NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
Adicional NMS 30* -
La pared de concreto de un frigorífico mide 3
m de alto, 5 m de ancho, y 20 cm de espesor. La
temperatura se mantiene en –10º C y la temperatura
exterior es 20º C. La pared interior está cubierta por
una capa de lana para reducir el flujo de calor a través
de la pared por 90 %. Las conductividades térmicas
del concreto y de la lana son 0,8 y 0,04 W/m.K,
respectivamente.
a) ¿Cuál es la diferencia de temperaturas de la capa
de lana?
b) ¿Cuál es el espesor de capa de lana requerido? |
|
| |
| Se trata de un ejercicio un poco complicado de aplicación de la Ley de Fourier, que describe la conducción del calor: |
|
|
|
|
|
Tenemos dos situaciones. En ambas la temperatura del frigorífico y del exterior se mantienen constantes. En la primera situación sólo hay una pared de concreto separando el interior del exterior del frigorífico. |
|
|
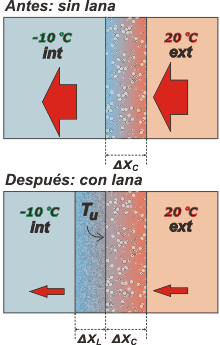 |
La ecuación que describe esta situación es ésta:
Q/ΔtA = – kC . A . ΔTT / ΔxC [1]
Donde Q/ΔtA es el flujo de calor por la pared de concreto en la situación inicial, sin lana; kC es la conductividad del concreto; A es el área de pared del frigorífico; ΔTT es la diferencia de temperatura entre el interior y el exterior; y ΔxC es el espesor de la pared de concreto.
Se ve que mantener frío el interior es muy costoso, entra mucho calor de afuera y las máquinas frigoríficas no dan abasto. Por eso pasamos a una segunda situación en la que se coloca una pared de lana pegada a la de concreto. El nuevo flujo, Q/ΔtD, disminuye en un 90% respecto al anterior.
Q/ΔtD = 0,1 . Q/ΔtA [2]
La situación después es un poco más complicada que la de antes, pero no mucho. |
|
|
|
| Lo más importante que hay que tener en cuenta es que la misma cantidad de calor que ahora atraviesa el concreto es la que también atraviesa la capa de lana: |
|
|
Q/ΔtDC = Q/ΔtDL = Q/ΔtD
|
[3] |
| Siendo: |
|
Q/ΔtDC = – kC . A . ΔTC / ΔxC
|
[4] |
Q/ΔtDL = – kL . A . ΔTL / ΔxL
|
[5] |
|
|
|
Donde ΔTC es la diferencia de temperatura entre las caras de la pared de concreto; y ΔTL es la diferencia de temperatura entre las caras de la pared de lana. No sabemos cuánto valen esas diferencias de temperatura porque desconocemos la temperatura de unión, TU, de ambas paredes. Y kL es la conductividad de la pared de lana.
Pero sabemos que la suma de las diferencias de temperatura en la pared de concreto, más la diferencia de temperatura en la pared de lana, no es otra cosa que la diferencia de temperatura entre el interior y el exterior.
ΔTT = ΔTC + ΔTL [6]
Con todo esto ya podemos ir al álgebra. Metamos la [1] y la [4] en la [2].
|
|
Tené presente:
ΔTT =
= -10ºC - 20ºC
ΔTC
=
= TU - 20ºC
ΔTL =
=-10ºC - TU
|
| |
– kC . A . ΔTC |
= 0,1 |
– kC . A . ΔTL |
|
|
| ΔxC |
ΔxC |
|
|
|
De ahí despejo ΔTC:
ΔTC = 0,1 . ΔTT
ΔTC = 0,1 . (-30 ºC)
ΔTC = -3 ºC
Y usando la [6]... |
|
|
|
|
 |
Para averiguar el espesor de la pared de lana podemos igualar la [4] con la [5]. |
|
| |
– kC . A . ΔTC |
= |
– kL . A . ΔTL |
|
|
| ΔxC |
ΔxL |
|
|
| Limpiamos un poquito y despejamos ΔxL. |
|
| |
kC . ΔTC |
= |
kL . ΔTL |
|
|
| ΔxC |
ΔxL |
|
|
| |
ΔxL= |
ΔxC . kL . ΔTL |
|
| kC . ΔTC |
|
|
| |
ΔxL= |
20 cm . 0,04 (W/m K) . 27 ºC |
|
| 0,8 (W/m K) . 3 ºC |
|
|
| |
|
| El principal componente aislante de la pared de lana es el aire atrapado entre las fibras, y no la fibra de lana misma. Aislarse con lana, con pelo, es el maravilloso invento de los mamíferos hace unos 150 millones de años. |
|
| * Tomado de Física 2, de Hugo Medina Guzmán, Lima, PUCP, 2009. |
|
|
Desafío:
¿Cuánto vale la temperatura de contacto entre las paredes? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Está absolutamente desaconsejado revelarle a un esquimal que su esposa nos hace ojitos. Agradezco a Cintia Perrone por el envío de una errata. Última actualización may-13. Buenos Aires, Argentina. |
|
|
| |
|
|
|

