 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
Adicional NMS 05 - Cuando un sistema evoluciona en forma reversible desde el estado A hasta el B por la evolución 1 (línea quebrada), como se representa en la figura, absorbe 3.440 J en forma de calor.
Encontrar:
A) El cambio de energía interna del sistema correspondiente a la evolución 2 (recta oblicua) desde B hasta A, indicando si aumenta o disminuye.
B) El calor intercambiado por el sistema en la evolución 2, indicando si lo cede o lo absorbe.
|
|
| |
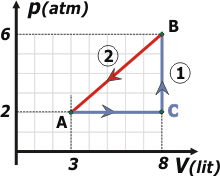
El enunciado venía con gráfico. Pero yo me adelanté, le puse color. Agregué el punto C, y una grilla en el fondo. Supongo que nos será más útil. |
|
|
La evolución en azul es la 1 (ACB) que en la tabla figura en celeste (o algo parecido) y está dividida en dos tramos: AC y CB. La evolución en rojo es la 2 (BA); en la tabla en la que voy volcando los datos le puse un color al tono.
Vamos a trabajar todo el ejercicio el l.atm, de modo que los 3.440 J debemos convertirlos, y eso nos da: 34 l.atm |
 |
|
|
|
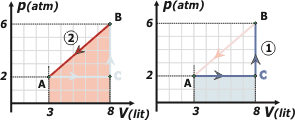
| Ya me adelanto y hago el cálculo de los trabajos de cada evolución. La isocora CB se corresponde con un trabajo nulo. El trabajo de B hasta A por la evolución 2, podemos calcularlo integrando el área encerrada bajo la curva 2. Se trata de un trapecio; podés calcularlo como la suma de un rectángulo más un triángulo. Y el trabajo AC se corresponde con el área del rectángulo sombreado en celeste. Mirá los gráficos de abajo. |
|
|
| El trabajo de la evolución 1 puede conocerse porque el trabajo de cualquier evolución es igual a la suma de los trabajos de cada tramo. |
| (l.atm) |
BA |
AC |
CB |
ACB |
| Q |
|
|
|
34 |
| L |
-20 |
10 |
0 |
10 |
| ΔU |
|
|
|
|
|
|
|
|
| Además, si el trabajo se corresponde con una disminución de volumen se tratará de un trabajo negativo (el medio realiza trabajo sobre el gas). |
|
|
Y si el trabajo se corresponde con un aumento de volumen se tratará de un trabajo positivo (el gas realiza trabajo sobre el medio).
Una parte importante del trabajo se resuelve haciendo sumas y restas. |
 |
|
|
|
Por ejemplo. La variación de energía interna en el tramo ACB debe cumplir con el primer principio de la termodinámica:
ΔUACB = QACB – LACB = 34 l.atm – 10 l.atm = 24 l.atm
|
|
|
Como la energía interna es una función de estado, su variación entre A y B debe ser igual y contraria a la variación entre B y A.
ΔUBA = – ΔUACB
|
| (l.atm) |
BA |
AC |
CB |
ACB |
| Q |
-44 |
|
|
34 |
| L |
-20 |
10 |
0 |
10 |
| ΔU |
-24 |
|
|
24 |
|
|
|
|
La calor intercambiado en la evolución BA surge entonces por aplicación del primer principio:
QBA = ΔUBA + LBA = – 24 l.atm + (–20 l.atm) = – 44 l.atm
Aunque no podemos conocer los valores de todas las magnitudes termodinámicas de las evoluciones, por lo menos, ya tenemos las respuestas a las preguntas del enunciado: |
|
|
A) ΔUBA = – 24 l.atm, disminuye; B) QBA = – 44 l.atm, cede. |
|
|
|
|
|
|
 |
| Desafío: Suponiendo que se trata de un gas ideal... ¿se podrá conocer la temperatura de los tres estados? |
|
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se recomienda fervientemente no hacer experimentos con gases explosivos ni malolientes, y menos aún, en presencia de mayores. Agradezco el envío de una errata a Candy Candy. Última actualización nov-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

