 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
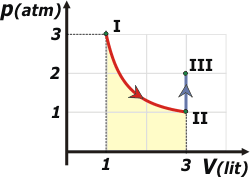
Adicional NMS 04 - Un gas se expande isotérmicamente desde el estado I de 3 atm de presión, volumen 1 litro y energía interna U1 = 456 J hasta el estado II donde su volumen es de 3 litros y su presión 1 atm. Se calienta entonces a volumen constante hasta el estado III en que su presión es de 2 atm y su energía interna U3 = 912 J.
A) Representar este proceso en un diagrama PV y calcular el trabajo realizado por el gas en cada etapa.
B) Determinar el calor absorbido o cedido durante este proceso.
|
|
| |
Ok, manos a la obra. Empecemos por el gráfico que, tenerlo hecho para pensar el ejercicio, es siempre una gran ayuda. Y es fácil. |
|
|
La transformación en rojo es isoterma, y la celeste es isocora. El área que sombré en amarillo representa el trabajo realizado por el gas en la transformación isoterma. En la isocora, lógicamente, el trabajo es nulo, ya que no hay variación de volumen.
Le puse una grilla al gráfico, que puede llegar a servirte: el área de cada cuadradito representa un trabajo equivalente a 1 l.atm. |
 |
|
|
|
| La otra herramienta de gran utilidad en los ejercicios de transformaciones de gases el la tabla de las evoluciones. Acá puse una: |
|
|
| Hay dos segmentos de naturaleza conocida (la isoterma que va desde I hasta II; y la isocora que va desde II hasta III. También puse una columna para la transformación total, que va desde I hasta III, cuyas magnitudes surgen de la suma de los tramos parciales. |
| (l.atm) |
I-II |
II-III |
I-III |
| Q |
|
4,5 |
|
| L |
|
0 |
|
| ΔU |
0 |
4,5 |
4,5 |
|
|
|
|
Ya completé las cosas obvias que surgen del enunciado: la variación de la energía interna durante la isoterma vale cero suponiendo que se trata de un gas ideal (abajo hago un comentario sobre este asunto). La variación de energía interna en la evolución total vale:
ΔUI-III = UIII – UI = 912 J – 456 J = 456 J = 4,5 l.atm
Y como
ΔUI-III = ΔUI-II + ΔUII-III
Nos queda que
ΔUII-III = 4,5 l.atm
El trabajo en la evolución isocora valía cero, ya te lo había dicho. Por lo tanto, como en todo tramo se cumple el primer principio de la termodinámica, tenemos que
QII-III = ΔUII-III + LII-III = 4,5 l.atm + 0 = 4,5 l.atm
Veamos qué otra cosa se puede calcular. Qué te parece el trabajo en la isoterma:
LI-II = n R T ln ( VII / VI )
Pareciera que necesitamos conocer n, el número de moles. Pero no es cierto, porque si asumimos que de un gas ideal se trata (tema del que te voy a hablar al final, ya te lo dije), entonces, usamos la igualdad que surge de la ecuación de estado:
n R T = P V
LI-II = PI VI ln (VII / VI) = PII VII ln (VII / VI)
LI-II = 1 atm 3 L ln (3 L / 1 L)
O, si querés...
LI-II = 3 atm 1 L ln (3 L / 1 L) = 3 l.atm . 1,1 = 3,3 l.atm
Si contás los cuadraditos que hay bajo la isotérmica, en el gráfico, verás que el resultado es muy razonable. |
|
|
El resto es una papa, porque en cada evolución (cada columna) se cumple el primer principio, entonces:
QI-II = 3,3 l.atm
|
| (l.atm) |
I-II |
II-III |
I-III |
| Q |
3,3 |
4,5 |
7,8 |
| L |
3,3 |
0 |
3,3 |
| ΔU |
0 |
4,5 |
4,5 |
|
|
|
|
| Y en cada evolución se cumple que la suma de las variaciones es la variación de la suma (sumas horizontales). |
|
|
QI-III = 7,8 l.atm (absorbido) |
|
|
|
DISCUSION: Vamos a discutir ese asunto del gas ideal. Si el gas de este ejercicio no fuese ideal, dos de las suposiciones que hicimos no tendrían validez (ya te marqué las dos suposiciones). En general los enunciados de estos ejercicios aclaran si se trata o no de un gas ideal. En éste no hay tal aclaración... por lo que hay que andarse con mucho cuidado.
Existen dos fuertes indicios de que se trata de un gas ideal. El primero es que los estado I y II están relacionados por la ley de Boyle-Mariotte:
PI . VI = PII . VII
Esa ley sólo la cumplen los gases ideales (aunque podría tratarse un una aproximación).
El otro indicio, más fuerte aún, es que la energía interna se duplica cuando se duplica la temperatura. De modo que la energía interna parece depender exclusivamente de la temperatura... y eso también lo cumplen los gases ideales. Mirá:
TII = PII VII / n R
TIII = PIII VIII / n R
Operando, surge que:
TIII = 2 TII
Y los datos del enunciado nos dicen que:
UIII = 2 UII
Ninguno de los dos indicios son concluyentes... pero son muy fuertes. |
|
|
| |
|
|
 |
| Desafío: Tampoco dice el enunciado si se trata de un gas monoatómico o diatómico o vaya-uno-a-saber-qué-tómico... ¿Se podrá averiguar? |
|
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se recomienda fervientemente no hacer experimentos con gases explosivos ni malolientes, y menos aún, en presencia de mayores. Última actualización nov-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

