 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
 |
41) Una máquina térmica con un rendimiento del 20% realiza un trabajo de 100 J en cada
ciclo. ¿Cuánto calor absorbe en cada ciclo?, ¿cuánto calor cede? |
|
| |
| A ver, a ver... primero: ¿tenés claro qué es lo que te indica ese esquema que te hice acá abajo y que aparece en todos los libros de termodinámica? |
|
|
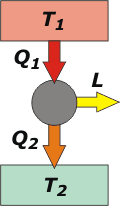 |
El círculo gris del centro es la máquina propiamente dicha. Como toda máquina, es gris-acero un poco sucia de aceite. El rectángulo de arriba es la fuente caliente, o sea, la caldera, que le entrega un calor, Q1, a la máquina (podría ser un chorro de vapor o alguna otra cosa con mucha energía). El rectángulo de abajo es el medio ambiente al que la máquina le tira el calor que no puede aprovechar, Q2 (por la chimenea, o el caño de escape, da lo mismo). L es el trabajo precioso que entrega la máquina, por eso le puse color dorado.
Ahora sí, vamos al ejercicio. La definición de rendimiento es
η = L / Q1
|
|
|
|
que por otra parte es muy razonable, ya que en cualquier lugar del mundo la idea de rendimiento es lo más parecido que puedas encontrar a la relación entre el beneficio de una empresa (en este caso una máquina) y la inversión que hiciste en el emprendimiento. Está claro que el beneficio de la máquina es el trabajo que nos brinda, L. Y la inversión es el combustible con el que calentás la caldera: el carbón, la nafta... Q1.
De modo que, despejando Q1:
Q1 = L / η = 100 J / 0,2
|
|
|
|
|
|
Nuestra máquina respeta las leyes de la termodinámica, si no... la denunciamos. No tiene alternativas:
QN = ΔU + L
El subíndice que le puse al calor corresponde a NETO. Porque el calor que intercambia la máquina... una parte lo recibe, otra parte lo cede, de modo que una parte irá sumando y a la otra le corresponderá ir restando. La variación de energía interna de la máquina es cero (ΔU = 0) si suponemos que no le cambia la temperatura mientras funciona (no hablamos del arranque sino del régimen estacionario del funcionamiento). La cosa queda así:
Q1 – Q2 = L
(Acordate que hemos convenido que el calor recibido es positivo y el calor cedido, negativo). Despejando Q2:
Q2 = Q1 – L = 500 J –100 J |
|
|
|
|
|
Otra manera de ver el primer principio es concentrarte en la máquina (el círculo gris del esquema) y pensar: todo lo que entra, sale. Bien, entran 500... deben salir 500. Así de fácil. |
|
|
 |
| Desafío: ¿Respetará nuestra máquina -tan prolija- el segundo principio de la termodinámica? |
|
| |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

