 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
 |
 |
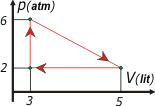
33) En la figura se muestra el gráfico p = p(V)
para un gas ideal que evoluciona
reversiblemente. Calcule para el ciclo
completo:
a) el trabajo realizado por el gas
b) el calor intercambiado
c) la variación de energía interna.
|
 |
| d) Para cada una de las evoluciones del
ciclo, indique cuáles de las magnitudes:
calor, trabajo y variación de energía
interna, pueden calcularse sin ninguna
suposición adicional y cuáles requerirían
suposiciones adicionales respecto a las
características del gas que evoluciona. |
|
|
| |
Es un ejercicio bastante sencillo, prestá atención. Voy a hacer una excepción a la norma de No me salen, en este ejercicio y en aras de la claridad, voy a trabajar sin las unidades correspondientes. De todos modos tendrás en cuenta que si llegamos a necesitar utilizar la constante de los gases ideales, elegiremos el valor que se corresponde con litros y atmósferas, o sea, 0,08207 l.atm/mol K.
En casi todos los ejercicios de evoluciones gaseosas suelo hacer un cuadro para ir volcando la información, ya que permite comprender fácilmente las deducciones por las que vamos transitando. Otra cosa que hago es ponerle nombres a los estados; los elijo arbitrariamente, cualquier nombre es válido. |
|
|
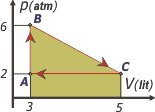 |
Ahora todo lo que voy calculando lo vuelco en la tabla (está más abajo). Por ejemplo, el trabajo de la transformación AB (isocórica) vale cero, ya que no hay variación de volumen.
El trabajo durante la transformación BC es igual al área encerrada bajo la curva (ojo, se trata de un área matemática, no geométrica: se mide en unidades de energía, no de superficie... y el cero del gráfico está desplazado... pero por suerte es un trapecio, o si preferís, la suma de un rectángulo más un triángulo) y vale 8 (latm, y no lo aclaro más). |
|
|
|
8 positivo, porque se corresponde con un aumento de volumen. No disponemos de una fórmula que no sea la integral para calcular ese trabajo ya que es realizado en una transformación cualquiera (el hecho de que evoluciones por una recta oblicua no reviste carácter especial alguno. Ese trabajo te lo sombreé en amarillo para que lo puedas apreciar correctamente. |
|
|
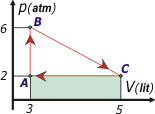 |
El trabajo en la transformación CA (una isobárica) podés calcularlo como
WCA = PCA . ΔV
y eso te da -4, lo cual es consistente ya que se corresponde con una disminución de volumen. Se trata de un trabajo realizado sobre el gas. Otro modo sencillo de calcularlo es integrando el área encerrada bajo la curva (en criollo: calculando el área igual que antes). |
|
|
Trabajo se puede simbolizar
L o W |
| El trabajo del gas en el ciclo completo se corresponde con el área encerrada en la gráfica del ciclo (que por suerte es muy sencilla de calcular ya que se trata de un triangulito. Vale 4, y debe tratarse de un trabajo positivo (hecho por el gas sobre el medio) ya que lo recorre en sentido horario. |
|
|
Vamos metiendo toda la información en el cuadro. Y de paso comprendiendo su funcionamiento: la suma de los tres primeros renglones (los pasos de la transformación) es igual al último (el ciclo cerrado total). Por ahora tenemos:
0 + 8 + (-4) = 4
|
| (latm) |
Q |
ΔU |
W |
| AB |
|
|
0 |
| BC |
|
|
8 |
| CA |
|
|
– 4 |
| ciclo |
4 |
0 |
4 |
|
|
|
|
Dentro de cada renglón también hay una lógica, que está dada por:
Q = ΔU + W
el primer principio de la termodinámica; de modo que la primera columna es igual a la suma de las dos restantes.
La variación de energía interna, ΔU, de un gas ideal a lo largo de un ciclo vale cero, ya que la energía interna es una función de estado, y el estado final es el mismo que el inicial. Por lo tanto el calor intercambiado por el gas en todo el ciclo debe valer 4, que es la suma de 0 más 4. (Son los dos números que ya había puesto en el cuadro y que responden con las tres primeras preguntas del enunciado).
Con los datos del ejercicio ya no podemos agregar mucho más. Pero el enunciado nos propone que agreguemos algunos datos que nos permitan calcular todas las magnitudes termodinámicas intermedias. |
|
|
Supongamos, entonces, que se trata de un mol, n = 1 mol, de un gas diatómico. Ahora podemos calcular, por ejemplo, la temperatura de cada estado:
TA = PA VA / n R = 73 K
TB = PB VB / n R = 220 K
TC = PC VC / n R = 122 K |
| (latm) |
Q |
ΔU |
W |
| AB |
30 |
|
0 |
| BC |
– 12 |
|
8 |
| CA |
– 14 |
|
– 4 |
| ciclo |
4 |
0 |
4 |
|
|
|
|
Conociendo las temperaturas (en realidad no son necesarias) podemos calcular los calores intercambiados en los procesos AB (isocórica) y CA (isobárica):
QAB = cv n ΔTAB = 2,5 . 0,082 . 1 . 147 = 30
QCA = cp n ΔTCA = 3,5 . 0,082 . 1 . (–49) = – 14
La lógica de la suma de los procesos (columnas) nos dice el el calor intercambiado en el proceso BC es -12, ya que:
30 + (-12) + (-14) = 4
|
|
Acordate que
cv = 2,5 R
cp = 3,5 R
son los calores molares específicos de un gas ideal diatómico, y R la constante de los gases ideales. |
Las variaciones de energía interna surgen de la aplicación del principio de conservación. Pero, también podríamos calcularlo directamente:
ΔUAB = cv n ΔTAB = 30
ΔUBC = cv n ΔTBC = – 20
ΔUCA = cv n ΔTCA = – 10 |
| (latm) |
Q |
ΔU |
W |
| AB |
30 |
30 |
0 |
| BC |
– 12 |
– 20 |
8 |
| CA |
– 14 |
– 10 |
– 4 |
| ciclo |
4 |
0 |
4 |
|
|
|
|
Y como yapa podés ver que la suma de las variaciones de energía interna a lo largo del ciclo es cero.
De modo que, ya sea por cálculo directo -cuando es posible realizarlo- o por complementariedad -tanto en la suma de procesos como en la conservación de energía- el cuadro de resultados se convierte en una herramienta de utilidad para resolver problemas de ciclos.
Nota: en vez de calcular previamente las temperaturas de cada estado, y luego sus diferencias, para realizar los cálculos de calor podríamos haber procedido de esta manera:
a V constante → n R ΔT = V ΔP
a P constante → n R ΔT = P ΔV
Entonces:
QAB = cv n ΔTAB = 2,5 R n ΔTAB = 2,5 VA,B ΔPAB = 30
QCA = cp n ΔTCA = 3,5 R n ΔTCA = 3,5 PC,A ΔVCA = – 14
Como ves, se llega a los mismos resultados pero no tuve que calcular las temperaturas, sólo utilicé los datos del enunciado. Lo mismo se podría haber hecho con los cálculos de variación de energía interna. O sea, tenelo a mano porque puede ser muy práctico. |
|
|
| |
 |
| Desafío: ¿Podrías calcular la equivalencia entre l.atm y cal? ¿Podrías agregar una columna más al cuadro y calcular las variaciones de entropía? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Laura Wepfer el envío de una errata. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

