|
NO ME SALEN
(APUNTES TEÓRICOS DE BIOFÍSICA DEL CBC)
ENTROPY
|
|

|
| |
ENTROPY, THE TIMELINE: THE MAGNITUDE THAT ALWAYS INCREASES
The Second Law of Thermodynamics (or just 2nd Law) becomes a strongly predictive law and with a very great potential of calculation thanks to the concept of entropy, denoted with S.
But what is entropy? I wasn't able to explain you what energy is and you want me to explain what entropy is ... no chance. I can give you some clues ... but the thing is that you are only going to arrive at a complete idea of the entropy by using it, measuring its changes, paying attention to what it tells us of each transformation of the universe... And don't just give up on it, because entropy is one of the most beautiful concepts in physics.
Related Ideas and Properties
- Entropy is related to disorder; some even say that entropy is a measure of the disorder of a system: and the more disorder there is, the greater the entropy.
- Increases in entropy are associated with energy degradation: useful energy, which can be transformed into work -for example- degrades to useless energy, which even being, cannot be exploited.
- Entropy is a scalar (like energy): it has no direction, is just a number with its units.
- When measuring entropy (same as with energy) its exact value in a particular time is not important.at, but what really matters is how much it increases or decreases, or if it remains constant, in a specific period of time. Most of the time it is not even possible to calculate the amount of entropy, S, but it is easy to know its variation (what really matters), ΔS.
- Entropy is a state function (such as P, V, T, U) which means that it has always the same value if the conditions don't change: it doesn't depend on the “history” of the system or the process that it performs (like Q, L).
Entropy Variation
It is the exhaustive sum of all the quotients between the small heat exchanges divided by the absolute temperature at which these exchanges were made, but with the condition that the heat has been exchanged in a reversible transformation… Too many words. Let's take a look on it: |
| |
| |
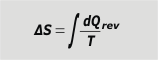 |
entropy variation |
|
|
|
If in the transformation whose variation of entropy we want to study, the temperature remained constant... then the integral sum is much simpler. |
|
|
| |
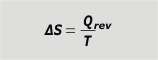 |
entropy variation with constant T |
|
|
|
Calculations of entropy variation are very useful, and in many cases you will be able to calculate it easily with that last definition. The international units for entropy are: [S] = J/K, (Joule divided by Kelvin). But what is Qrev?
Reversible heat, Qrev
There is no reversible heat ... don't get scared. It’s the name given to the heat exchanged on a reversible transformation. But actually reversible transformations neither exists… now you can get scared. In our universe it is forbidden to “go in reverse”. A small portion of the universe can go back (for example: nothing prevents you from reading this note from the beginning because you realized that it needs to be read more carefully) ... but the universe as a whole can't.
And if reversible transformations don't exist ... what do we mean when we talk about them? We are referring to that impassable boundary, to which we can approach but never transcend. That is called an ideal transformation.
It may happen that a transformation occurs without heat exchange. Can you calculate the entropy variation for that process? Yes: you have to know the initial and final state of the process, and imagine any reversible evolution (there may be more than one possible) that connects them. This evolution will surely have nothing to do with the original, but the entropy variation will be the same, since entropy is a state function (it does not depend on the "path" the system has taken).
What are the characteristics of these ideal, reversible transformations? In this article I describe them with a little more detail, but what interests you for the purposes of calculation is that ideal transformations are carried out through a succession of defined states, where all the parameters that describe the transformation (eg temperature, pressure, volume, etc.) are known with certainty.
Entropy and the Second Law
The formulation of the Second Law of Thermodynamics, which implies the entropy, says in barely words: in any transformation, the entropy of the universe increases: |
|
|
|
|
|
Pay attention to this really simple example. |
|
|
 |
You fill a glass, half with hot water (ac) and half with cold water (af). The heat that the hot water gives to the cold water, is equal to the heat that the cold water receives from the hot water. After the mix, both "parts" of the glass end up with the same temperature.
The cold water increased its entropy and the hot water diminished it. However, in absolute value, the increase of the cold water entropy is greater than the decrease of the hot water… Then, the total entropy of the system will have increased.
Where did that extra entropy come from? The answer is that it was created during the mixing process. And you cannot go back: that amount of newly created entropy can no longer be destroyed: the universe must bear that increase for eternity. In symbols:
|
|
|
|
ΔSac + ΔSaf > 0 (con ΔSac < 0 y ΔSaf > 0 )
The sign of the entropy variation (that is, if it increases or decreases) is given by the numerator of the definition of entropy variation, since the denominator (the absolute temperature) is always positive. Therefore, if a body yields heat, its entropy will decrease (ΔS <0) and if a body receives heat, its entropy will increase (ΔS> 0).
Variation of entropy in a thermal machine
The application of the 2nd Law (entropy version) to the operation of a thermal machine results surprisingly descriptive: |
|
|
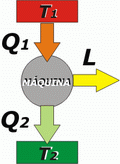 |
There are three bodies present in this phenomenon: the hot source, the cold source and the machine itself. Then, the total entropy variation, that is, the entropy variation of the universe, will be equal to the sum of the entropy variations of each body:
ΔS1 + ΔSM + ΔS2 > 0
The machine operates cyclically by constantly returning to the same state. Therefore, its entropy does not change, ΔSM = 0. |
|
|
|
The other two bodies, because they are sources, don't vary their temperature, what will make the calculation of their entropy variation much easier: |
|
|
|
|
|
Q1 is a heat yielded by the hot source, therefore, for the purpose of calculating the entropy variation of the hot source, that heat is negative. |
|
|
|
|
|
All thermal machines operate in such a way that the quotient of the wasted heat divided by the temperature at which the loss occurs is greater than the quotient of the heat taken from the hot source divided by the temperature of the source.
How much greater needs to be the first member?
The Second Law doesn't say it ... it says only that it has to be greater. 3 times greater, twice, 1.2 times, 0.1 times greater, 0.00001 times... the limit (by definition, but not real) of this reasoning is that the quotients can become equal. That limit situation is called ideal.
But in an ideal machine, a perfect machine, the first member will be equal to the second one. And that machine would transform caloric energy into mechanical energy in a reversible and ideal way, and with the maximum efficiency possible. In that ideal machine that discovered the French Sadi Carnot well before the 2nd law was postulated, it would be true that...
|
|
|
|
|
|
Or what is the same: |
|
|
|
|
|
And its efficiency (the maximum possible) would be: |
|
|
| η = 1 – |
Q2 |
= 1 – |
T2 |
|
|
|
| Q1 |
T1 |
|
|
|
When engineers saw this conclusion they quickly went on to manufacture machines with warmer boilers, and better cooling radiators. Industries moved to the margins of rivers or seacoasts. The industrialists filled their pockets and the planet began to warm. Please don't heat up with this. |
|
|
| |
|
|
| Entropy ... is not what it used to... |
|
|
| |
|
|
CURIOUS FACTS |
|
|
- The word "entropy" in physics was first used by Rudolf Clausius in 1854.
- Here's another definition of entropy: it is the state function that measures the probability for a closed system to approach to thermal equilibrium.
- And another one, even more statistical: the increase of the entropy indicates the passage of a system from a less probable state to a more probable state.
- The first one who pointed out that valuing entropy was equivalent to valuing disorder was Hermann von Helmholtz (1821-1894).
- Another simple way to measure the increase in entropy is to quantify waste, garbage, and environmental pollution. Economists often forget that the 2nd Law never rests. There is no completely clean production, waste is always generated. You cannot produce, produce and produce without contaminate, contaminate and contaminate.
- Sigmund Freud read something about the increase of the entropy in the universe and from there derived the theory of the death instinct. And millions of people believed it! I'm not kidding!
|
|
|
CAPTIOUS QUESTIONS |
|
|
- Some scientists described the phenomenon of life thermodynamically in the following way: life is a machine to reduce entropy; Generating more life means lessening entropy. Poetically: a desperate cry of matter against entropy. This is a very nice and realistic description, but ... Doesn't this violate the second principle?
|
|
 |
| |
|
| Some rights reserved. Reproduction permitted if quoting the source. Last updated on Feb-17.Translated by Esteban Djeordjian. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|