|
NO ME SALEN
THEORETICAL NOTES AND EXERCISES OF
PHYSICS AND BIOPHYSICS
Dynamics
|
|

|
Center of mass
We already know that most of the bodies have their mass distributed within the bodies’ volume. But in a lot of cases they act as if their whole mass was reunited in one point. That point is what we call the center of mass, G, and it’s a very intuitive concept, as most people can easily predict the posicion of the center of mass, xG, of many bodies in many situations.
|
 |
|
|
You have surely realised by now that the center of mass isn’t necessarily found inside the body, as in the case of the ring, a hollow ball, a chair, etc.
There is however an analytical method to find this center of mass and so that you understand it I’m going to demonstrate this from a very easy situation. Imagine a body (more accurately: A system of masses) constituted by two identical punctual masses. Where can we find the center of mass here? |
|
|
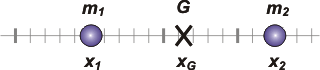 |
|
|
That’s right: midpoint of the two positions! That point we can deduce by averaging from each body’s own position: |
|
|
|
|
|
Now let’s imagine a different scenario… In which the mass of the second body is greater than of the first body. Where will the center of mass be now? This certainly isn’t a tough one: Along the line that connects the two masses and closer to the bigger one. But, where exactly? |
|
|
 |
|
|
The expression that refers to this is called weighted arithmetic mean (we give more “weight” to the heavier portion of the system) |
|
|
| xG = |
|
m1 x1 + m2 x2 |
|
|
| m1 + m2 |
|
|
|
|
In which M is the total mass of the system, say, the sum of the mass portions among the system’s volume. As hard as it may be to believe, that position is independent of the frame of reference you decide to use.
If we want to make this general for any number of stealthy corpuscles: |
|
| xG = |
|
m1 x1 + m2 x2 + m3 x3 + ... + mi xi |
|
|
| M |
|
|
Once again, M is the total mass of the body/system. Let’s summarize this as: |
|
|
|
|
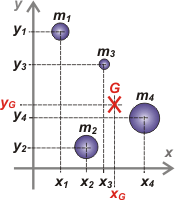
The rest is easy. If the mass is distributed along a surface we’ll find the center of mass coordinates, xG and yG , operating the same way as before but now focusing on individual axes. |
|
|
Shall we?
xG = ( Σ mi xi ) / M
yG = ( Σ mi yi ) / M
And the mass distributing system will now take place in a 3D volume, like all real bodies, so we’ll proceed the in the same way but now within a three-dimensional frame of reference, with 3 axes, taking into account the volume of the body. That should look something like:
xG = ( Σ mi xi ) / M
yG = ( Σ mi yi ) / M
zG = ( Σ mi zi ) / M
|
 |
|
|
|
You may object: what even are these bodies, whose massive parts are away from each other… The answer is as follows: matter’s nature is corpuscular; as compact as you may believe a body is, it’s actually mostly made up by hollow space, its mass concentrated in distant particles. If it weren’t because of the attraction and repulsion forces generated between these particles, bodies could trespass one another with rare chances of having particles collide. We could trespass walls, infiltrate bank’s vaults… but then again, we wouldn’t be able to make love.
On the other side, this idea of mass unevenly distributed through a body offers us a neat method to find the center of mass of non-geometrical or non-uniform bodies (usually the most painful to deal with). This method consists of cutting up the body (mentally) in portions whose masses are easy to calculate and whose centers of mass (of the portion) are easy to determine. Then we would have a body ideally constituted by discrete and maneuverable portions of point particle… |
|
| If the nucleus of an atom (that reunites 99% of all of the mass) had the size of a soccer ball, the electrons would be the size of a grain of sand and would be spinning around the ball at thousands of feet away. |
|
|
|
|
| Important Gossip: |
|
|
- The hardest trial Newton had to face when defending his Law of Universal Gravitation was that any celestial object (the Moon, the Earth) would behave as if it’s entire mass was reunited and found in a single point (the infamous center of mass). To overcome this…he invented mathematical analysis (son of a…!)
- The center of mass is due to some interesting properties. E.g. the balance of two bodies supporting each other is determined by considering the center of mass: balance exists if this center is found along the vertical line that goes through the supporting area
- Another property is that forces applied in the same direction the center of mass is found will cause no rotation on the body
- “Particle Systems” (as galaxies, planetary systems, explosion’s fragments) are a pain to describe, lay out, or solve if we analyze the dynamic superposition of each particle… we can instead set the eye on the system’s center of mass… there we have a far easier task.
|
|
|
| Trick Questions: |
|
 |
- What’s the difference between center of mass and center of gravity?
- Can it be that barycenter is the same as center of mass? Are they synonyms? How do we get to a triangle’s barycenter?
|
|
| |
|
| Translated by
Román Dumas. Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last Updated Jun-15. Buenos Aires, Argentina. |
|
|
 |
|