 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo, energía cinética)
|
|

Video de este ejercicio

Video del anterior
 |
 |
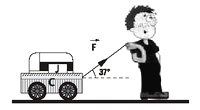
1.5- Nicolás corre 4 m tirando de su carrito,
con la caja de juguetes encima, con la fuerza
constante de 30 N en la dirección indicada en la
figura. (Ver Ej. 2.39 de Dinámica).
El carrito tiene 10 kg y la caja 2 kg, y el rozamiento
entre el carrito y el piso es despreciable. Calcular: |
 |
|
| a- |
El trabajo que realiza la fuerza de rozamiento
sobre la caja J.
|
| b- |
El trabajo que realiza cada una de las fuerzas
que actúan sobre el carrito |
| c- |
La velocidad que alcanza cada objeto, si al
partir estaban en reposo. |
|
|
|
Por el orden en que están formuladas las preguntas y la disponibilidad de datos, me da la impresión que el autor del problema supone que vas a ir a ver el problema 2.39 de dinámica y vas a utilizar los datos disponibles y hallados ahí. Pero, si alteramos el orden, podemos responder todas las preguntas con lo que aparece acá y nada más. |
|
|
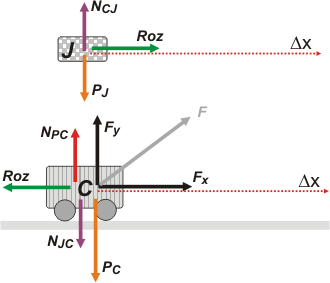 |
En este ejercicio hay rozamiento entre el carrito y el juguete.
Pero no hay rozamiento entre el carrito y el piso... no te confundas. |
Apliquemos directamente la definición de trabajo que conocemos (WF = F Δx cos α), ya que todas las fuerzas que actúan son constantes. Empiezo por el juguete.
WRoz = Roz 4 m cos 0º
No podemos calcularla porque no sabemos cuánto vale el rozamiento (a menos que chusmeemos el problema 2.19). El resto de las fuerzas que actúan sobre el juguete forman 90º con el desplazamiento por lo tanto su trabajo vale cero.
Vamos al carrito. El trabajo de la fuerza que hace Nicolás es very easy.
WF = 30 N . 4 m . cos 37º
|
|
|
|
|
|
Como la resultante de todas las fuerzas sobre el conjunto carrito-juguete es FX (tené presente que tanto el rozamiento -como las otras fuerzas de contacto- son internas del sistema carrito/juguete... tenés que considerarlo como un cuerpo único), podemos aplicarle (al conjunto) el teorema de la resultante. Acordate, además, que
FX = F cos 37º
De hecho, la definición de trabajo WF = F . Δx . cos α es equivalente a WF = FX . Δx
WRes = ΔEc
FX . Δx = ½ mTot vF² — ½ mTot v0²
Al partir estaban en reposo...
96 J = ½ 12 kg vF²
|
|
|
|
|
|
Ahora vuelvo al juguete. Y aplico el mismo teorema de recién, pero para el juguete la resultante es la fuerza de rozamiento, y sólo ella. De modo que
WRoz = ½ mJ vF²
WRoz = ½ 2 kg ( 4 m/s)²
|
|
|
|
|
|
| Quedaba pendiente una parte de la pregunta del enunciado que se refería a los trabajos sobre el carrito (ahí el rozamiento y el desplazamiento forman 180 grados). |
|
|
|
|
|
Todas las demás fuerzas que actúan sobre el carrito son perpendiculares al desplazamiento de modo que el trabajo que realizan es nulo. Y chau. |
|
 |
| DESAFIO: ¿Qué ocurriría si no hubiese rozamiento entre el carrito y el juguete? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

