WORK

The word “Work” in physics is not the same as in the colloquial language. The fundamental difference is that in colloquial language work is the product of a person’s effort (or animal or machine). In Physics, work is an attribute of a force (I will come back to this, which is very important). Work is usually represented by an L or W, then a sub index identifies the force to which the work belongs. For example, W_F (work of the force F) or W_Res  (work of the Resultant) and so on.

So for a nonzero work to exist there must be a displacement of the body on which force is exerted. For example in the following situation:

Work can be defined as follows (for constant forces only):

where F is the magnitude (intensity) of the force, Δx is the modulus (length) of  the displacement, and α is the angle between force and displacement.

Work is a scalar, or a number (plus units) that shows us how much a force adds to the body’s movement. Unlike a force, work has no direction or sense, it’s not a vector but a scalar.

The units in which work is measured must arise from the product of the units in which forces are measured (Newton) by the units in which displacements are measured (meter). Cosine has no units.

[W] = N . m = J    (Joule)

Due to its relevance the unit of Work is named after the English physicist James Prescott Joule (1818-1889). We will meet him again later.

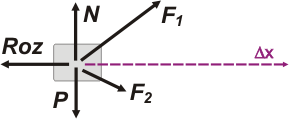
Let’s assume we have a body that moves a certain space Δx under several forces acting simultaneously.

As the work is an attribute (a feature, a magnitude) of the forces I could compute the work for each one, for instance the work of F1, or of P or N... W_F1, W_F2, W_P, W_Roz(frictional), W_N... are all magnitudes, in principle, calculable. But if I ask for the work of the body, or the work of the observer ... these questions have no physical sense.

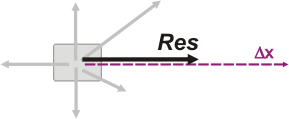
Even the resultant for all acting forces, although not an interaction in the Newtonian sense of the word, it remains a force with all the attributes of the forces. Therefore I wonder if the work of the resultant W_Res  is also, in principle, calculable.

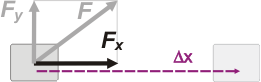
As F . cos α is the force component pointing in the direction of travel (usually called F_X) the definition could be written as:

Represented by:

Notice that this definition (which is fully equivalent to the first) does not take into account the work of the component of F perpendicular to the displacement, Fy. But this is entirely consistent with the original definition, since Fy  form an angle of 90° with  the displacement then the cosine of 90° is 0 and so is the work it produces.

IMPORTANT GOSSIP:

• Were forces not constant then the work can be computed by splitting the movement as much as possible, so that each fraction change in strength is negligible. Then add up all of the work fractions and... behold the work. This strategy can be represented as follows:

  W_F = ∫ F dx cos α

  The fact that the work is the integral sum of the product between the differential force and displacement indicates that another way to calculate work would be computing areas enclosed under the curve on the F-x graphics..

• Two vectors can be multiplied in two different ways: scalar product, which is the mode used to find work; and there is also the vector product, which is the other mode, and when used, the result of the multiplication is a vector. The latter is not our case.

TRICKY QUESTIONS:

• What is the work of a force perpendicular to the displacement?

• Since the definition of work uses only the modules of the vectors involved, what determines the sign of the work?. When work is negative?

• Could it be that erg  (erg), cal  (cal), eV  (electron volt) and l.atm (liter atmosphere) are also units for work? (This is driving me crazy).