 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular) |
|
|

|
| |
FIS 59 (d3.12) - Una curva de autopista de 300 m de radio no tiene peralte (inclinación en la curva que
permite realizar giros a mayor velocidad sin correr el riesgo de salirse de la pista). Un camión cuyo
peso es de 14000 kgf transita la autopista. El coeficiente de rozamiento estático entre los
neumáticos y el asfalto seco es de 0,75, en el asfalto mojado es de 0,50, y en el hielo es de 0,25.
a) Determinar la máxima rapidez con la que se puede pasar la curva con toda seguridad (sin
deslizar) en: (i) días secos, (ii) días lluviosos y (iii) días helados.
b) Suponer que no hay rozamiento. Con las velocidades calculadas en a), calcular, en cada caso, el
ángulo del peralte para que el vehículo se mantenga sin salirse de la curva.
c) Recalcular las velocidades halladas en a), si la autopista tiene un peralte de 3°.
d) ¿Cómo cambiarían las velocidades calculadas en el punto a) si en vez de camiones se tratase de
motocicletas o de autos?
|
|
Más largo que esperanza de pobre... Si no tiene peralte, la autopista es horizontal, entonces la fuerza que hace que el camión tome la curva sin despistarse es la fuerza de rozamiento estática. Las velocidades máximas serán funciones de las fuerzas de rozamiento estáticas máximas, o sea de los coeficientes de rozamiento estático.
RozeM = m aC
μe . N = m vmáx² / R
De donde:
vmáx² = μe . m . g . R / m
vmáx² = μe . g . R
|
|
|
| |
vmáx/seco = 47 m/s
vmáx/mojado = 39 m/s
vmáx/hielo = 27 m/s |
|
|
|
|
Eso es 170 km/h, 140 km/h, y 97 km/h. Esas velocidades tan altas no se permiten (al menos en las autopistas argentinas), pero son posibles gracias a que el radio de la curva es grande, una de las propiedades de las aytovías rápidas.
Vamos al los peraltes.
b) Suponer que no hay rozamiento. Con las velocidades calculadas en a), calcular, en cada caso, el
ángulo del peralte para que el vehículo se mantenga sin salirse de la curva. Para entender cómo una inclinación de la curva -el peralte- puede reemplazar al rozamiento, vamos a hacer el DCL. |
|
|
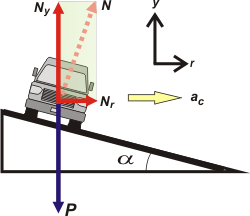
Ahí tenés nuestro camión pegando la curva en una autopista peraltada. La fuerza que produce la aceleración centrípeta, aC, es el apoyo sobre el asfalto, la normal, N (normal al piso) que se proyecta hacia el centro de la curva: Nr. (r por dirección del radio).
Tenés que trabajar un poquito geométricamente, pero sin mucho esfuerzo llegarás a comprender que:
Nr = N sen α
Ny = N cos α
|
 |
|
|
|
Y por otro lado, Newton nos asegura que:
Nr = m . vmáx² / R
Ny = m . g
El resto es pan comido:
N sen α = m . vmáx² / R
N cos α = m . g
Las divido miembro a miembro:
tg α = vmáx² / R g
Y calculo α para cada una de las velocidades que teníamos en el ítem anterior. |
|
|
| |
αseco = 36°
αmojado = 27°
αhielo = 14° |
|
|
|
|
Son inclinaciones muy pronunciadas, ninguna ruta ni autopista se construye de esa manera, porque claro, siempre contamos para doblar con la fuerza de rozamiento. El ítem siguiente plantea una inclinación más razonable.
c) Recalcular las velocidades halladas en a), si la autopista tiene un peralte de 3°. En este caso tenés que considerar que tenemos la ayuda del peralte y también el rozamiento (con los coeficientes indicados en el enunciado). Vamos al nuevo DCL. |
|
|
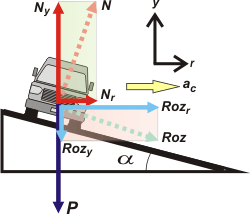
Ahí va de vuelta el mionca. La fuerza de rozamiento siempre es paralela a las superficies, de modo que la tenemos que descomponer:
Rozr = Roz cos α
Rozy = Roz sen α
Y las metemos en las de Newton:
Nr + Roz cos α = m . vmáx² / R
Ny = m . g + Roz sen α
|
 |
|
|
|
| Las combinamos algebraicamente (no me hagas laburar tanto)*... |
|
|
| vmáx² = R g |
|
sen α + μe cos α |
|
|
| cos α — μe sen α |
|
|
|
| Y calculamos las 3 velocidades máximas para cada coeficiente estático y α = 3°. |
|
|
| |
vmáx/seco/p = 50 m/s
vmáx/mojado/p = 41 m/s
vmáx/hielo/p = 30 m/s |
|
|
|
|
Si las comparás con las anteriores, te das cuenta que con apenas una inclinación de 3 grados de peralta (casi indetectable) las velocidades críticas (para no despistarse) aumentan sensiblemente.
Para responder la última pregunta: d) ¿Cómo cambiarían las velocidades calculadas en el punto a) si en vez de camiones se tratase de
motocicletas o de autos? Alcanza con que cambies la masa del camión por la masa de la moto en nuestra fórmulas finales... ¡¡Jajajaja!!
|
|
|
*Si no pudiste resolver el álgebra para hallar la expresión de la velocidad máxima, podés verla acá.
Nota: el asunto del peralte con y sin rozamiento lo tenés analizado con mayor detalle y profundidad en este ejercicio y en este otro. |
|
 |
| DESAFIO: ¿Se puede reolver el ejercicio con SR paralelo a la calzada? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Karen Calvo por el envío de una errata. Última actualización abr-16. Buenos Aires, Argentina. |
|
|
|
|

