 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Tiro oblicuo)

|
|

|
NMS c5.17* - Un objeto se lanza en tiro oblicuo desde el origen de coordenadas. En un instante pasa por el punto (2 m; 3 m) y en otro por el (5 m; 2 m). Calcular la velocidad inicial y el ángulo de inclinación del disparo.
Como siempre, empecemos con un esquema: |
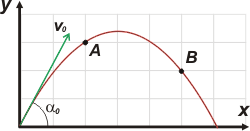 |
Llamemos A al primer punto mencionado en el ejercicio, y B al segundo. El objeto pasa por ellos en los instantes tA y tB.
La velocidad inicial (representada en verde en una escala arbitraria que no tiene nada que ver con la escala de posiciones) tendrá una componente horizontal, vx, y otra vertical, voy. |
|
|
| cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia |
|
Todo tiro oblicuo se describe con dos ecuaciones de posición (una de posiciones horizontales y otra de alturas) y una de velocidades verticales a la que, en este ejercicio, le daremos descanso. Por si no tenés a mano los modelos, te los transcribo acá: |
|
|
x = xo + vx ( t – to)
y = yo + vo ( t – to) + ½ g ( t – to)²
|
modelos
(para cualquier TO) |
Para hacer que esos modelos describan el movimiento de este ejercicio en particular, basta con reemplazar las constantes iniciales (to , xo , yo , vx , voy , y g) por las de nuestro movimiento. Algunas no sabemos cuánto valen... pero por lo menos tienen el nombre correcto y ya vamos a averiguar su valor. |
|
| nuestro TO: |
x = vx t |
| y = voy t – 5 m/s² . t² |
|
ecuaciones
(que describen todo el movimiento narrado en el enunciado) |
| Ahora les pedimos a las ecuaciones que hablen de los eventos interesantes de los que pueden hablar: las posiciones A y B. |
|
| en el instante A |
2 m = vx tA |
[1] |
| 3 m = voy tA – 5 m/s² . tA² |
[2] |
| en el instante B |
5 m = vx tB |
[3] |
| 2 m = voy tB – 5 m/s² . tB² |
[4] |
|
ecuaciones especializadas
(sólo hablan de los momentos interesantes del movimiento) |
Y a dónde te creés que llegaste: a un sistema de tantas ecuaciones como incógnitas en donde algunas de ellas son las que te pide el enunciado del ejercicio. No inventamos nada, no hicimos para este planteo nada que no hayamos hecho para todos los ejercicios de cinemática... El resto es álgebra. Es muy importante que visualices este límite entre la física y el álgebra. Si lo hacés... ya podés ir sintiéndote físico... porque te lo ganaste.
Por supuesto: hay mil maneras de resolverlo. Yo te muestro una... pero no te olvides que a partir de acá se trata de un ejercicio algebraico. De las ecuaciones [1] y [3] despejamos los instantes de tiempo y eso lo metemos en las [2] y [4]. Así ya desaparecen los instantes... que no nos interesan porque no nos lo preguntan.
tA = 2 m / vx
tB = 5 m / vx
Vamos despacito, no te pierdas:
3 m = ( voy 2 m / vx ) – 5 m/s² . (2 m / vx)²
2 m = ( voy 5 m / vx ) – 5 m/s² . (5 m / vx)²
Despejo voy de cada una:
voy = 1,5 vx + ( 10 m²/s² / vx )
voy = 0,4 vx + ( 25 m²/s² / vx )
Y ahora las igualo, y despejo vx
1,5 vx² + 10 m²/s² = 0,4 vx² + 25 m²/s²
1,5 vx² – 0,4 vx² = 25 m²/s² – 10 m²/s²
1,1 vx² = 15 m²/s²
vx² = 13,64 m²/s²
vx = 3,69 m/s
Todo el resto es cuesta abajo: reemplazo vx en [1] y [3], y averiguo tA y tB.
tA = 0,542 s
tB = 1,355 s
Con ellos voy a las ecuaciones [2] y [4], y averiguo voy verificando que en ambas me da el mismo valor.
voy = 8,25 m/s
La velocidad inicial la obtengo componiendo -por Pitágoras- las componentes que obtuve; y el ángulo de inclinación inicial, con el arcotangente del cociente voy /vx. |
|
| |
| |
| |
|
|
|
| |
|
|
Discusión: Esto es un aburrimiento total: todos los ejercicios de cinemática salen de la misma manera, haciendo siempre lo mismo, sin necesidad de invertir una gota de inteligencia, ni creatividad, ni nada... ¡así no vale! |
|
|
| Desafíos: Hallar en qué instante alcanza la altura máxima y en cuál otro retorna al piso. |
|
 |
| |
|
| *Mi agradecimiento a Juan Andrés Ferreyra por acercarme este interesante ejercicio. Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

