 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Análisis matemático
|
|

|
| Funciones derivadas |
| |
La derivada de una función es otra función. Esta nueva función se deriva (se infiere, se obtiene) de la primera, y de ahí su nombre.
Pero la forma en que se obtiene asegura que la derivada tiene un significado muy especial y por demás útil. Sea una función y(x), su función derivada, y'(x), describe para todo x la rapidez con la que cambia y a medida que cambia x.
Esto puede parecer un contrasentido ya que cuando decimos para todo x, se trata de un x individual, puntual, exclusivo; y cuando decimos cambio de x aludimos al menos a dos x, o mejor aún a un grupo de x... pero no a uno solo.
Pero no hay tal contrasentido, y eso es gracias a una de las proezas del análisis matemático: la capacidad de hacer converger un intervalo (de lo que sea) a un único elemento. |
| Tal vez un ejemplo ayude a aclarar las cosas: supongamos que tenés una función que describe las posiciones de un móvil en cualquier instante de tiempo. Esa función se podría simbolizar así x(t). Su función derivada nos indicaría con qué rapidez va cambiando la posición en todo instante de tiempo, y justamente, esa es la función velocidad v(t). Incluso podemos volver a derivar esta función velocidad y encontrar una nueva que nos indicaría cómo va variando la velocidad en cada instante de tiempo, y esa nueva función no es otra que la aceleración, a(t). Y así podríamos seguir. |
|
La función derivada se distingue de su original -o primitiva- con un apóstrofe o prima. Si una función se designa f(x), su función derivada: f'(x). |
|
|
En nuestro ejemplo cinemático:
x(t). (Función que describe la posición).
x'(t) = v(t). (Función que describe la velocidad).
x''(t) = v'(t) = a(t). (Función que describe la aceleración).
|
|
| La derivada se define de esta manera: |
|
|
|
Y en palabras matemáticas se lee así: la derivada es el límite para cuando el incremento de la variable independiente tiende a cero, del cociente entre un incremento de la función sobre el incremento de la variable independiente. Más resumidamente: el límite para Δx tendiendo a cero del cociente incremental. (Δy/Δx es el cociente incremental).
Si ya hiciste un curso de análisis matemático y límites, habrás hecho muchos ejercicios de límite de cocientes y recordarás que esos límites no siempre existen o que quedan indeterminados. Es sorprendente que muchas funciones que describen fenómenos físicos, sus derivadas también describen fenómenos físicos.
El ejemplo arquetípico de la física en las que las derivadas hablan de cuestiones relevantes es la cinemática, en la que la función principal describe la posición de un móvil en cualquier instante de tiempo. Si derivamos esa función (sea la que sea) la función que obtenemos describe la velocidad del móvil en cualquier instante de tiempo. Y si volvemos a derivar esta función, la nueva derivada que obtenemos (segunda derivada de la primera) describe la aceleración del móvil en cualquier instante de tiempo.
Diferenciales. Si Δx tiende a cero la diferencia se convierte en un diferencial, y se simboliza dx. De modo que la derivada también se puede simbolizar de esta manera: |
|
|
|
|
|
Que es muy práctica porque los diferenciales tienen autonomía algebraica, o sea los puedo multiplicar, dividir, cancelar o lo que sea con total independencia uno de otro.
La derivada y la tangente. Una confusión habitual con las derivadas consiste en creer que la derivada es una función lineal, una recta, y que además, es tangente a una curva. Eso no es cierto. Sólo en algunos casos muy especiales la función derivada es una función lineal (una recta). (En cinemática es el caso del MRUV). La función derivada de la posición se representa con una curva que en principio nada parece tener que ver con la curva que representa a la función primitiva. Pero mirá este ejemplo. |
|
|
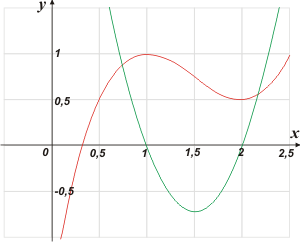 |
En rojo la función original:
y(x) = x³ − 4,5x² + 6x − 1,5
Y en verde su derivada:
y'(x) = 3x² − 9x + 6
Sólo a los ojos expertos podés encontrar algo que tenga que ver con tangentes.
Como ves a simple vista, la derivada es la ecuación de una parábola, no de una recta. |
|
|
|
La clave es ésta: el valor que toma la función derivada es igual a la pendiente (tg α) o inclinación que tiene la función original en ese punto (y no en otro), que se observa mejor si trazás la tengente a ese punto. (En el ejemplo las tracé en celeste). |
|
|
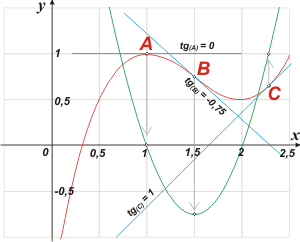 |
Mirá el punto A de la función original: y(1) = 1. Ahí (justo ahí) la curva no está inclinada. Si mirás el valor de la derivada: y'(1) = 0, ella nos indica la pendiente (el ángulo de inclinación) de la función, ya que la tangente vale 0 cuando el ángulo vale 0.
Mirá al punto B: y(1,5) = 0,75. En ese punto la curva está inclinada hacia abajo, y si miramos la derivada (la parábola en este caso) podremos saber en qué ángulo está inclinada:
y'(1,5) = −0,75, o sea que está inclinada unos 36,87 grados hacia abajo, ya que tg(-37°) = -0,75.
|
|
|
|
Ahora mirá el punto C de la función: y(2,25) = 0,609. Se ve que en C la función se inclina hacia arriba... cuánto valdrá su pendiente en ese punto. Si mirás la función derivada ves que en ese punto vale... y'(2,25) = 1, luego en ese punto la inclinación de la curva es de 45 grados. (tg 45° = 1)
Resumiendo: la derivada de una función en un punto cualquiera representa a la pendiente de la recta tangente a la función en dicho punto. |
|
|
| Chismes importantes |
|
|
- Un poco de historia. Las derivadas (y todo el resto del cálculo matemático) lo descubrieron -o inventaron- paralela en independientemente Isaac Newton y Gottfried Leibniz. Newton, que antes que matemático era físico, visualizó inmediatamente la furibunda importancia que tenían las derivadas en la descripción de universo. Y se enamoró a primera vista. Las llamó fluxiones, y extrapoló la cinemática a toda la matemática llamando velocidad a lo que hoy día llamamos (más correctamente) cociente incremental. Ponele.
- Los diferenciales son cantidades muy pequeñas. Cuánto de pequeñas, y mirá, no sé cómo decirlo, probemos así: son cantidades que tienden a cero. Los matemáticos dicen: son cantidades infinitesimales (infinitamente pequeñas). Cuando yo estudiaba les decíamos pendejésimos.
- Las derivadas de las derivadas también dan información sobre la primitiva de la primitiva. Por ejemplo, si derivás nuestra parábola y''(x) = 6x − 9 se trata de una recta que corta las x en 1,5. Eso nos indica que la función original tiene ahí un punto de inflexión (su tangente es muy especial, porque es una tangente que no es tangente... es secante, jijiji). (Parece un chiste pero no lo es).
- El ángulo de la tangente sólo es visualizable como tal cuando las escalas x e y son iguales (1:1, como en nuestro ejemplo), por eso preferimos utilizar la palabra derivada, que no nos remite necesariamente a un ángulo. Y cuando se trata de funciones físicas (como posición y velocidad) no hay que graficarlas juntas y el valor numérico de las pendientes no se corresponde con ningún ángulo geométrico.
|
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

