NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
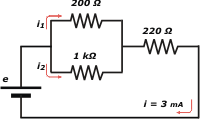
32) En el circuito de la figura, la corriente i es de 3 mA.
a) ¿De qué intensidad son las corrientes i1 e i2?
b) ¿Cuánto vale la diferencia de potencial entre los extremos
de cada uno de los resistores?
c) ¿Cuál resistor requiere más potencia? Explique. |
 |
|
| |
| Un súper clásico más. Lo voy a resolver en forma integral, o sea, voy a encontrar los valores de todas las corrientes, no solamente la que pide el enunciado. De ese modo te muestro cómo se procede para cualquier circuito. |
|
|
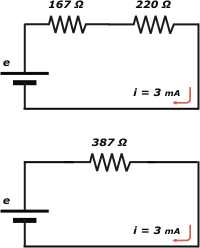 |
Yo tengo como costumbre ir simplificando el circuito, paso a paso hasta obtener el más simple de todos los circuitos posibles, o sea, aquel que tiene una sola resistencia, una sola corriente y una sola fuente.
La resistencia de 200 Ω y la de 1.000 Ω se hallan en paralelo. De modo que voy a reemplazar ese par por su equivalente:
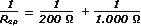
Rep = 167 Ω
Ahora es todavía más fácil, porque las dos resistencias que quedan se hallan claramente en serie. Las voy a reemplazar por su equivalente:
Res = 167 Ω + 220 Ω = 387 Ω
|
|
|
|
A este circuito -equivalente al primero pero más sencillo- lo sometemos al detector de mentiras de la Ley de Ohm: e = ΔV = i . R
e = 3 mA . 387 Ω = 1,16 V
También puedo conocer la diferencia de potencial en cada una de las resistencias de la serie.
ΔV220Ω = 3 mA . 220 Ω = 0,66 V
ΔV167Ω = 3 mA . 167 Ω = 0,50 V
Como ves, se cumple que la suma de las diferencias de potencial a lo largo del circuito es igual a la diferencia de potencial de la pila.
Ahora, sabiendo que la diferencia de potencial en la resistencia de 167 Ω es 0,50 V puedo conocer las corrientes que pasan por las resistencias de 200 Ω y 1.000 Ω, que están bajo la misma diferencia de potencial.
i1 = 0,50 V / 200 Ω = 2,5 mA
i2 = 0,50 V / 1.000 Ω = 0,5 mA
|
|
|
|
|
|
|
Nuevamente, chequeamos, con el concepto de que la suma de las corrientes que pasan por esas dos resistencias debe ser igual a la corriente que pasa por su equivalente. Y ocurre.
Para responder la segunda pregunta podés calcular (yo no te lo voy a hacer) la potencia disipada en cada resistencia (Pot = i² R) y fijarte cuál es la más alta.
ATENCIÓN: andan por ahí circulando en apuntes, fórmulas para calcular intensidades de corriente y otras variables eléctricas en circunstancias particulares. Los autores de esos apuntes las llaman fórmulas salvadoras. Supongo que las llaman salvadoras porque sirven -según ellos- para aprobar un examan. Es cierto que, tal vez, aumenten en cierta proporción la probabilidad de aprobar... pero definitivamente aseguran que no aprendas física. Es como si fueras al natatorio a aprender a nadar y el profesor de natación te dijera: mirá, es más fácil si vas caminando por el borde de la pileta. |
|
|
| |
|
 |
| Desafío: Ya que te hice calcular la potencia en cada resistencia... ¿podrías decirme cuánto vale la potencia de la fuente sin hacer nuevos cálculos? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Lucia Julia Guccione por el envío de una errata. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

