NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
3) An infinite plane is charged in such a way that the electric field |E| = 2,25 103 N/C for a spot 3mm away from the plane.
a) Draw the field lines.
b) Calculate the electrical potential difference for two spots 5m and 7m away from the plane. Does the previous result change if the indicated spots are over the same field line?
c) Calculate the kinetic energy gained by an electron when it moves 1cm from rest. |
|
| |
Infinite… what a word, so enigmatic, so borgian… There you have the drawing for a field generated for an homogeneous distribution charge on an… infinite plane. Logically, I could only draw a part of it: the gray base plane, in which you can find charges in every direction and never reach the border. And the field lines, all so straight, parallel and perpendicular to the plane… they are also infinitely long and stretching up never reaching an end!! (I had to cut them because I was afraid you didn’t have a screen that long… besides, I took advantage of the cut and, there, I drew an arrow end that indicates that the field lines have an orientation). |
|
|
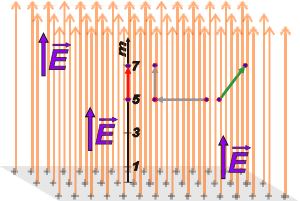 |
You can imagine – obviously – that such a field and such a plane do not actually exist… But usually it’s not a bad approximation for small scale situations. In those cases physicists save words and say that the plane is infinite… in essence, they are poets.
So, as you can see, and as you can imagine the lack of borders, the field is constant and uniform… its value is always the same and points always in the same direction regardless of where you are, 3 m from the plane or 25. |
|
|
|
And its constant value in any position will be the same:
E = 2,25 x 10³ N/C
Or also:
E = 2,25 x 10³ V/m
But don’t forget t is a vector, and what is written above is just the modulus, its numerical value. In the drawing I depicted it three times: in a position 3 m away from the plane and in two other different positions, and always with a vector the same length, the same direction and the same sense… in other words, constant.
We can find the electrical potential between two spots at 5 y 7 m as the product between the field value and the difference in position:
ΔV5-7 = E . Δx
ΔV5-7 = 2,25 x 10³ V/m . 2 m
|
|
| The formulation is not that clear. What it is asking is the electrical potential between the 5 and 7 meter levels. |
|
|
|
|
You must have realized that we would have obtained the same value if we had calculated the electrical potential between meters 9 and 11. And the answer wouldn’t have changed either if the spots had been in different lateral positions as the arrows I drew in green and gray. In fact, the electrical potential between any pair of spots situated at the same distance from the plane, is zero. This group of spots among which the electrical potential is null, form “potential equalization planes” (they have the same electrical potential).
The kinetic energy, Uc, of an electron (or any charge) that moves inside an electrical field can be found by multiplying the field value, the charge and the displacement (which in this case is perpendicular and towards the plane).
Uc = E . e- . Δx
Uc = 2,25 x 10³ N/C . 1,602 x 10-19 C . 0,01 m
|
|
|
|
|
|
We could have also calculated it as the product between the charge and the electrical potential between both positions:
ΔV1cm = E . Δx = 2,25 x 10³ V/m . 0,01 m = 22,5 V
Uc = ΔV1cm . e- = 22,5 eV
The electron-volt, eV, is a very small amount of energy equivalent to…
1 eV = 1,602 x 10-19 J
So I guess both results are the same, can you check? |
|
|
| |
|
 |
| Challenge: ¿What’s that electron’s speed? |
|
| |
|
Translated by Alcides Pinto. Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last updated mar-14. Buenos Aires, Argentina.
|
|
| | |
|
|