NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
2) a) The intensity of the electric field E due to a charge Q at the point where a charge Q’ > Q is situated is grater, lower or equal to that of the electric field E’ due to the charge Q’ at the same point where Q is situated?
b) Same question for the intensities of forces F (exerted by Q on Q’) and F’ (exerted by Q’ on Q). |
|
| |
If you don’t mind, and for the sake of clarity, I’m going to call the bigger charge QG and the smaller one Qch. The same for fields and forces. I will also arbitrarily choose charges of equal sign, both positive. Anyway, all I will say is valid for any combination of charges and independent of their signs. |
|
|
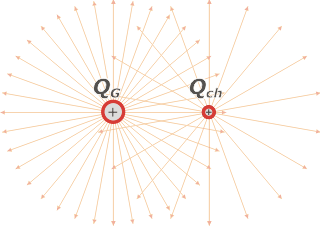 |
In this figure I show both charges in space, each one in the vicinity of the other.
I also show the electric field spectrum that each charge would produce on its own. But beware: it’s not the field spectrum created by both! In electric fields, field lines never cross. |
|
|
|
| However, an overlapping fields graph is useful because it’s one of the ways in which you can know the form of the field generated by both charges (shown in the last figure, bellow). And because, physically, it makes sense: the field at any spot is the vector sum of the fields generated by each of the charges affecting that spot. |
|
|
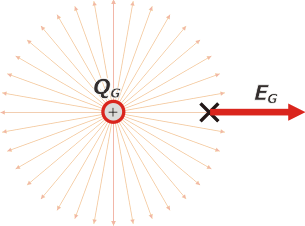 |
Here I show the field generated by the big charge in the position occupied by the small one.
That vector is proportional to the big charge: |
|
| ko is Coulomb’s constant, and d is the distance between the charge and the position in which the field is calculated (in other words, in this case, the distance between the charges). |
|
|
|
| Let’s go now to the field generated by the small charge in the position occupied by the big charge. |
|
|
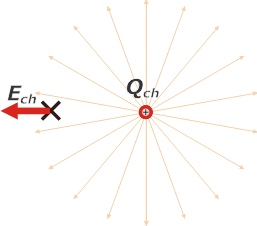 |
Just as I represent it, the field Ech is represented by a shorter vector than the one for EG.
The definition of field clearly states that: |
|
And being QG > Qchthere is no other possibility that: |
|
|
|
|
|
|
In the following figure you can see both charges and the electric field generated between both over the surrounding space. Also, I represented the repulsion force that each charge exerts on the other one. |
|
|
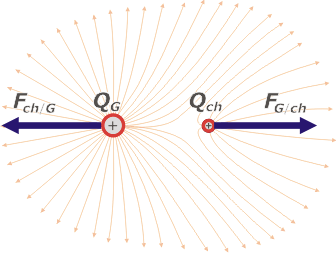 |
As for the intensity of the force that each charge exerts on the other… it’s a tricky question.
Electric forces – as all other forces – are always half of an interaction between two bodies (in this case: two electric charges repelling each other). |
|
|
|
The force that the big charge exerts on the small one has the exact same intensity and direction, and opposite sense, as the force that the small charge exerts on the big one. |
|
|
|
|
|
Both forces are an interaction couple. (I’m sure that, at this point, you had that clear).
In fact, they are both calculated the same way: |
|
|
| Fch/G = FG/ch = |
|
ko QG Qch |
|
|
| d² |
|
|
|
| This is nothing else than Coulomb’s law, that gives us the magnitude of the electrostatic forces (always, between a pair of charges). And as you know: the order of factors does not alter the value of the product, that is, it’s the same calculation for both. |
|
|
| |
|
 |
| Challenge: How does the field look from a faraway position? |
|
| |
|
Translated by Alcides Pinto. Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last Updated nov-13. Buenos Aires, Argentina.
|
|
| | |
|
|